บทความนี้จะเจาะลึกว่าความสมดุลของพุต/คอลคืออะไร สูตรที่แน่นอนในการคำนวณ และการทำความคุ้นเคยกับแนวคิดนี้จะช่วยให้คุณเข้าใจตลาดออปชั่นได้ลึกซึ้งยิ่งขึ้นอย่างไร
Put/Name Parity คืออะไร?
ความเท่าเทียมกันระหว่างราคาขายและราคาซื้อคือแนวคิดที่กำหนดความสัมพันธ์ทางคณิตศาสตร์ระหว่างราคาของออปชั่นขายและออปชั่นซื้อที่มีราคาใช้สิทธิ์และวันหมดอายุเท่ากัน กล่าวอีกนัยหนึ่ง หากออปชั่นซื้อมีการซื้อขายที่ X ออปชั่นขายที่มีราคาใช้สิทธิ์และวันหมดอายุเท่ากันก็ควรมีการซื้อขายที่ Y และในทางกลับกัน
หากพูดให้เข้าใจง่ายๆ ก็คือ ความสมดุลของการวาง/การเรียกจะทำให้คุณสามารถใช้ชุดค่าผสมที่แตกต่างกันของตัวเลือกเพื่อสร้างตำแหน่งเดียวกันได้ และทำให้ความสัมพันธ์ทางคณิตศาสตร์ระหว่างการวางและการเรียกเป็นทางการมากขึ้น
ตัวอย่างเช่น การรวมหุ้นอ้างอิงกับออปชั่นขายแบบ at-the-money นั้นแทบจะเหมือนกับการซื้อออปชั่นซื้อแบบ at-the-money เลยทีเดียว ออปชั่นขาย/ออปชั่นซื้อนั้นถือว่าพอร์ตโฟลิโอที่เหมือนกันทั้งสองนี้ควรมีต้นทุนเท่ากัน
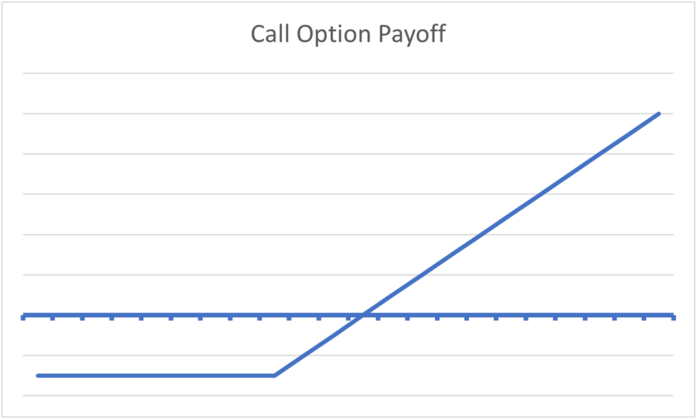
เพื่อให้คุณเห็นภาพได้ ทั้งตำแหน่ง “เรียกแบบสังเคราะห์” และการซื้อออปชั่นซื้อโดยตรงต่างก็มีผลตอบแทนที่เท่ากัน ดังที่คุณจะเห็นในแผนภาพผลตอบแทนด้านล่าง:
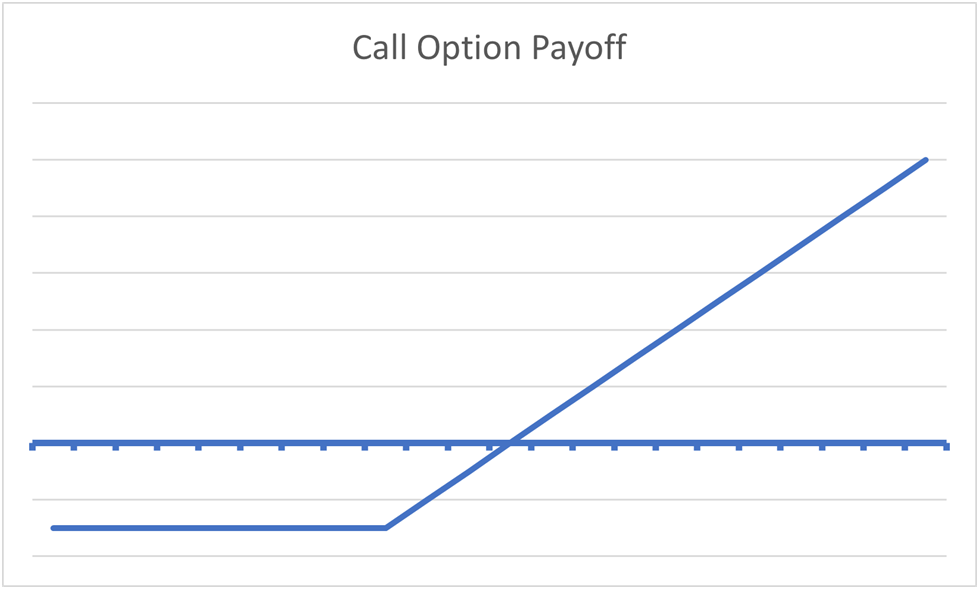
ความสมดุลระหว่าง Put/Name จะทำให้การคำนวณทางคณิตศาสตร์เบื้องหลัง Put และ Name เป็นทางการ และให้มูลค่าที่แท้จริงที่ชัดเจนแก่ตัวเลือกแต่ละตัว การนำระบบสังเคราะห์มาใช้หมายความว่าตัวเลือกแต่ละตัวจะมีส่วนประกอบของการเก็งกำไรโดยตรง ซึ่งช่วยให้ผู้ซื้อขายที่ฉวยโอกาสสามารถรักษาราคาตัวเลือกให้อยู่ในระดับที่เหมาะสมได้เสมอ
ตัวอย่างเช่น โอกาสในการเก็งกำไรโดยปราศจากความเสี่ยงจะเกิดขึ้นหากสามารถซื้อออปชั่นซื้อแบบสังเคราะห์ได้ในราคาที่ถูกกว่าออปชั่นซื้อโดยตรง ซึ่งจะจูงใจให้ผู้ซื้อขายดันราคากลับมาที่มูลค่าที่เหมาะสม
สูตรการใส่/เรียกแบบสมดุล
ความเท่าเทียมกันระหว่างการขาย/การซื้อมีสูตรที่ตรงไปตรงมามาก ซึ่งทำให้คุณสามารถกำหนดราคาตามมูลค่าที่เหมาะสมของออปชั่นการขายเมื่อเทียบกับออปชั่นการซื้อที่เทียบเท่า (มีราคาใช้สิทธิและวันที่หมดอายุเท่ากัน) และในทางกลับกัน
ความเท่าเทียมกันของราคาขาย/ซื้อนั้นใช้ได้กับออปชั่นที่มีราคาใช้สิทธิ์และวันที่หมดอายุเท่ากันเท่านั้น ตัวอย่างเช่น เมื่อใช้สูตรนี้ คุณสามารถเปรียบเทียบราคาใช้สิทธิ์ขายและซื้อที่ราคาใช้สิทธิ์ 101 ดอลลาร์ซึ่งทั้งคู่จะหมดอายุใน 21 วัน แต่คุณไม่สามารถเปรียบเทียบราคาใช้สิทธิ์ขายและซื้อที่ราคาใช้สิทธิ์ 101 ดอลลาร์ที่มีวันหมดอายุต่างกันได้
ความสมดุลของการซื้อ/ขายมีดังนี้:
C + PV(x) = P + S
ที่ไหน:
ค = ราคาของออปชั่นซื้อ
P = ราคาของออปชั่นขาย
PV (x) = มูลค่าปัจจุบันของราคาใช้สิทธิ์
S = ราคาปัจจุบันของสินทรัพย์อ้างอิง
มาลองแทนค่าตัวเลขจริงลงในสูตรและลองดูกัน เราจะเริ่มด้วยราคาของสินทรัพย์อ้างอิง
ลองสมมติว่าสินทรัพย์อ้างอิงมีการซื้อขายที่ 61.66 ดอลลาร์ และเรากำลังดูออปชั่นซื้อที่ราคาใช้สิทธิ์ 70 ดอลลาร์ ซึ่งมีการซื้อขายที่ 1.45 ดอลลาร์ และจะหมดอายุใน 25 วัน
ดังนั้นมาแก้ไขสูตรของเราโดยแทนค่า $1.45 สำหรับ C ซึ่งเป็นราคาของออปชั่นซื้อ และ $61.66 สำหรับ S ซึ่งเป็นราคาของสินทรัพย์อ้างอิง
1.45 + PV(x) = P + 61.66
ตอนนี้เราเหลือค่าอีกสองค่าที่จะต้องพิจารณา PV(x) หมายถึงมูลค่าปัจจุบันของราคาใช้สิทธิ์ แต่สิ่งนั้นหมายความว่าอย่างไร เนื่องจากออปชั่นเป็นข้อตกลงในการซื้อหรือขายในราคาที่ระบุในวันที่ในอนาคต เราจึงต้องลดราคาใช้สิทธิ์ให้เท่ากับปัจจุบันเพื่อคำนึงถึงมูลค่าของเงินตามเวลา เราใช้อัตราดอกเบี้ยที่ปราศจากความเสี่ยง (โดยทั่วไปคืออัตราดอกเบี้ยต่อปีของตั๋วเงินคลังสหรัฐฯ อายุ 3 เดือน) เพื่อลดราคาใช้สิทธิ์ให้เท่ากับปัจจุบัน ในขณะที่เขียนนี้ อัตราดังกล่าวอยู่ที่ 4.7% ดังนั้นการคำนวณทางคณิตศาสตร์จะมีลักษณะดังนี้:
PV(x) = S / (1 + r)^T
ที่ไหน:
S = ราคาใช้สิทธิ์ของสินทรัพย์อ้างอิง
R = อัตราดอกเบี้ยปลอดความเสี่ยงเป็นทศนิยม
T = เวลาหมดอายุเป็นปี เป็นทศนิยม
หากต้องการแปลงเวลาหมดอายุให้เป็นทศนิยม เราเพียงหารเวลาหมดอายุด้วย 365 เช่น 25/365 = 0.068
ดังนั้นสูตรของเราจะมีลักษณะดังนี้:
PV(x) = 70 เหรียญ / (1 / 0.047)^0.068 = 69.79 เหรียญ
ดังนั้นมูลค่าปัจจุบันของราคาใช้สิทธิ์จึงเท่ากับ 4,076.16 ดอลลาร์ ลองแทนค่าสุดท้ายลงในสูตรของเรา:
1.45 + 69.79 = พี + 61.66
ดังนั้นในการแก้ปัญหาสำหรับ P หรือราคาของออปชั่นขายที่ใช้สิทธิ์เดียวกันและหมดอายุเท่ากัน เราจะรวมราคาออปชั่นซื้อและมูลค่าปัจจุบันของสิทธิ์ ซึ่งจะได้ 71.24 จากนั้นเราจะลบราคาสปอตของสินทรัพย์อ้างอิงออกจาก 71.24 ซึ่งก็คือ 9.58
สูตรความสมดุลของราคาซื้อ/ขายที่ได้รับการคิดค้นขึ้นในช่วงทศวรรษ 1960 ยังมีข้อจำกัดสำคัญบางประการในยุคปัจจุบัน
การปรับสมดุลระหว่าง Put/Name ใช้กับออปชั่นยุโรป
สูตรดั้งเดิมของราคาซื้อ/ขายที่ Hans Stoll นำเสนอในปี 1969 นั้นใช้ได้กับออปชั่นยุโรปโดยเฉพาะ เมื่อแนะนำออปชั่นสไตล์อเมริกัน การคำนวณจะเปลี่ยนไปเล็กน้อย เพราะคุณสามารถใช้สิทธิ์ได้ทุกเมื่อจนกว่าจะหมดอายุ
หากคุณต้องการคุ้นเคยกับความแตกต่างมากขึ้น โปรดอ่านบทความของเรา การชำระตัวเลือกซึ่งจะเจาะลึกถึงความแตกต่างระหว่างตัวเลือกแบบยุโรปและอเมริกัน
แต่โดยสรุปแล้ว ออปชั่นของยุโรปจะเป็นแบบชำระด้วยเงินสด และสามารถใช้ได้เมื่อหมดอายุเท่านั้น ตัวเลือกอเมริกัน มีการชำระเงินทางกายภาพ ซึ่งหมายความว่าการชำระเงินนั้นเกี่ยวข้องกับการโอนสินทรัพย์อ้างอิงตามจริง และสามารถใช้ได้ตลอดเวลาจนกว่าจะหมดอายุ
ออปชั่นดัชนีและฟิวเจอร์สเป็นแบบยุโรป ในขณะที่ออปชั่นหุ้นเป็นแบบอเมริกัน
ยังคงมีความสัมพันธ์แบบ put/name parity ในออปชั่นอเมริกัน คณิตศาสตร์จะแตกต่างกันเล็กน้อย ดูสิ่งเหล่านี้ บันทึกการบรรยายของ NYU เพื่อดูการแยกรายละเอียดของคณิตศาสตร์
การซื้อ/ขายแบบสมดุลไม่ได้คำนึงถึงเงินปันผลหรือการจ่ายดอกเบี้ย
ประเด็นต่อไปคือสูตรความสมดุลระหว่างการขายและการซื้อจะไม่คำนึงถึงกระแสเงินสดที่เกิดขึ้นจากการถือสินทรัพย์อ้างอิง เช่น การจ่ายดอกเบี้ยหรือเงินปันผล ซึ่งสิ่งเหล่านี้ยังทำให้การคำนวณเปลี่ยนแปลงไปด้วย
หากคุณนำพันธบัตรหรือหุ้นที่จ่ายเงินปันผลมาใส่ในสูตรขาย/ซื้อหุ้น คุณจะพบว่าตัวเลขจะไม่ตรงกัน นั่นเป็นเพราะสูตรนี้ไม่ได้คำนึงถึงมูลค่าปัจจุบันของกระแสเงินสด เช่น เงินปันผลหรือการจ่ายดอกเบี้ย คุณสามารถดัดแปลงสูตรเพื่อให้ใช้กับกระแสเงินสดได้เช่นกัน แต่ขั้นตอนนี้อยู่นอกเหนือขอบเขตของบทความนี้
ความสมดุลของการซื้อ/ขายไม่รวมต้นทุนหรือค่าธรรมเนียมในการทำธุรกรรม
สุดท้ายนี้ ความสมดุลของการซื้อ/ขายจะไม่นำค่าใช้จ่ายในการทำธุรกรรม ภาษี ค่าคอมมิชชันหรือค่าใช้จ่ายภายนอกอื่นๆ เข้ามาพิจารณา
การจำลองแบบสังเคราะห์
ในบทนำของบทความนี้ เราได้พูดถึงวิธีการใช้ชุดตัวเลือกที่แตกต่างกันเพื่อสร้างพอร์ตโฟลิโอสองพอร์ตที่มีผลตอบแทนเท่ากัน เราได้กล่าวถึงว่าการรวมออปชันขายและหุ้นอ้างอิงจะให้ผลตอบแทนเท่ากับการซื้อออปชันซื้อ
ไอเดียนี้เรียกว่า การจำลองแบบสังเคราะห์คุณสามารถสร้างตำแหน่งที่มีผลตอบแทนและโปรไฟล์ความเสี่ยงที่เหมือนกันได้ แม้ว่าจะมีชุดหลักทรัพย์ที่แตกต่างกันก็ตาม การทำความเข้าใจเกี่ยวกับหลักทรัพย์สังเคราะห์อย่างคร่าวๆ จะทำให้ผู้ซื้อขายออปชั่นเข้าใจถึงธรรมชาติที่แท้จริงของออปชั่นได้ดีขึ้น และเข้าใจว่าออปชั่นสามารถผสมผสานกันได้อย่างไรเพื่อเปลี่ยนมุมมองทางการตลาดของคุณ
การใช้องค์ประกอบพื้นฐานของการขายหรือซื้อแบบระยะสั้น/ระยะยาวและการขายแบบระยะสั้น/ระยะยาวของสินทรัพย์อ้างอิง ช่วยให้คุณสามารถจำลองตำแหน่งออปชั่นได้เกือบทุกตำแหน่ง ต่อไปนี้คือตัวอย่างพื้นฐาน:
สังเคราะห์ยาว อ้างอิง: พุตสั้น + คอลยาว
สั้นสังเคราะห์ อ้างอิง: การขายแบบขาย + การขายแบบขาย
คอลแบบสังเคราะห์: คอลแบบอิงระยะยาว + คอลแบบพุตระยะยาว
Artificial Brief Name: สัญญาซื้อขายระยะสั้น + สัญญาซื้อขายระยะสั้น
สัญญาซื้อขายแบบ Lengthy Put: สัญญาซื้อขายแบบ Brief Underglow + สัญญาซื้อขายแบบ Lengthy Name
สัญญาซื้อขายระยะสั้นแบบสังเคราะห์: สัญญาซื้อขายระยะสั้นแบบยาว + สัญญาซื้อขายระยะสั้นแบบสั้น
จากตรงนี้ เราจะมาพูดคุยกันถึงการแปลงค่า การกลับตัว และการกระจายกล่อง ซึ่งล้วนเป็นกลยุทธ์การเก็งกำไรที่เทรดเดอร์ใช้เพื่อแสวงหากำไรจากราคาออปชั่นเมื่อราคาเบี่ยงเบนจากราคาออปชั่นที่ซื้อขายกันตามปกติ โปรดจำไว้ว่าเทรดเดอร์ทั่วไปจะไม่ทำการซื้อขายเหล่านี้ แต่การเรียนรู้วิธีการทำงานของกลยุทธ์เหล่านี้จะช่วยให้คุณเข้าใจตลาดออปชั่นได้ดีขึ้น
การซื้อ/ขายแบบสมดุล: จุดเริ่มต้นของคณิตศาสตร์ตัวเลือก
เพื่อให้คุณเข้าใจพื้นฐานได้คร่าวๆ ย้อนกลับไปในช่วงทศวรรษ 1960 ตลาดออปชั่นมีขนาดเล็กมาก แม้แต่นักเทรดที่เฉียบแหลมที่สุดก็ยังไม่รู้ว่าจะกำหนดราคาออปชั่นอย่างไร และนั่นก็เหมือนกับโลกตะวันตกที่ไร้ขอบเขต Hans R. Stoll เป็นหนึ่งในนักวิชาการไม่กี่คนที่เจาะลึกถึงรายละเอียดของการกำหนดราคาออปชั่นในบทความสำคัญของเขา ความสัมพันธ์ระหว่างราคาออปชั่นขายและซื้อ ตีพิมพ์ในปีพ.ศ.2512–
งานของเขามีขึ้นก่อนงานของโมเดล Black-Scholes อันล้ำสมัยของ Black, Scholes และ Merton ในปีพ.ศ. 2516
Stoll พบว่าบางครั้งสามารถซื้อตำแหน่งสังเคราะห์เหล่านี้ได้ในราคาที่ถูกกว่าตำแหน่งจริง ตัวอย่างเช่น หากตลาดหุ้นมีแนวโน้มขาขึ้นอย่างมากและผู้ซื้อขายกำลังซื้อออปชั่นซื้อ คุณสามารถซื้อออปชั่นอ้างอิงด้วยราคาที่เท่าราคาตลาด และสร้างออปชั่นซื้อสังเคราะห์ในราคาที่ถูกกว่าการซื้อออปชั่นซื้อที่เท่าราคาตลาด โดยพื้นฐานแล้ว ตลาดออปชั่นมีการเก็งกำไร ซึ่งตลาดออปชั่นจะไม่มีประสิทธิภาพ
หลักการของการไม่เก็งกำไร
ความเท่าเทียมกันของการขาย/การซื้อเป็นแนวคิดพื้นฐานในการกำหนดราคาออปชั่น ซึ่งถือว่าพอร์ตโฟลิโอสองพอร์ตที่มีผลตอบแทนเท่ากันควรมีราคาเท่ากัน
นี่คือการขยายแนวคิดที่สำคัญที่สุดแนวคิดหนึ่งในทฤษฎีทางการเงิน นั่นคือ หลักการไม่เก็งกำไร พูดง่ายๆ ก็คือ แนวคิดที่ว่าคุณไม่สามารถทำกำไรโดยปราศจากความเสี่ยงได้โดยการใช้ประโยชน์จากความไม่มีประสิทธิภาพของตลาด
หากจะเชื่อมโยงสิ่งต่างๆ โดยตรงกับ put/name parity ภายใต้กฎของการไม่เก็งกำไร คุณไม่ควรสามารถจำลองผลตอบแทนของพอร์ตโฟลิโออื่นและซื้อได้ในราคาที่ถูกกว่า ตัวอย่างเช่น หุ้นสังเคราะห์ควรมีราคาเท่ากับการซื้อหุ้นอ้างอิง
โมเดลการกำหนดราคาอนุพันธ์ทั้งหมดใช้หลักการไม่มีการเก็งกำไรเป็นสมมติฐานในตัว ซึ่งทำให้โมเดลสามารถประมาณการได้ตามความเป็นจริงทางเศรษฐกิจที่ผู้ซื้อขายจะใช้ประโยชน์ และปิดโอกาสในการเก็งกำไรอย่างแท้จริงเมื่อเกิดขึ้น
บรรทัดสุดท้าย
ความสมดุลระหว่างการซื้อและการขายเป็นแนวคิดพื้นฐานที่ผู้ซื้อขายออปชั่นระดับกลางทุกคนควรทำความคุ้นเคยโดยทั่วไปแล้ว t เป็นกรณีที่สามารถสร้าง name/put ใดๆ ขึ้นมาใหม่ได้โดยใช้ทางเลือกของหุ้นบวกกับ put/name (ตามลำดับ) การเข้าใจความสมดุลของราคาซื้อ/ขายจะไม่สามารถสร้างรายได้ให้กับเทรดเดอร์ได้ แต่การเรียนรู้แนวคิดเหล่านี้เป็นส่วนหนึ่งของการพัฒนาความตระหนักรู้ที่กว้างขึ้นว่าตลาดออปชั่นทำงานอย่างไร
บทความที่เกี่ยวข้อง
สมัครสมาชิก SteadyOptions เลยตอนนี้และสัมผัสประสบการณ์การซื้อขายออปชั่นที่เต็มประสิทธิภาพได้เพียงปลายนิ้วสัมผัส คลิกปุ่มด้านล่างเพื่อเริ่มต้น!