ขอขอบคุณแอนดรูว์มิลเลอร์เป็นพิเศษสำหรับการโจมตีครั้งนี้และ Zack Hess, Vlad Zamfir และ Paul Sztorc สำหรับการอภิปรายและคำตอบ
หนึ่งในความประหลาดใจที่น่าสนใจยิ่งกว่าใน cryptoeconomics ในช่วงไม่กี่สัปดาห์ที่ผ่านมามาจากการโจมตี schellingcoin ตั้งครรภ์โดย Andrew Miller เมื่อต้นเดือนนี้ แม้ว่าจะเป็นที่เข้าใจกันอยู่เสมอว่า schellingcoin และระบบที่คล้ายกัน (รวมถึงความก้าวหน้ามากขึ้น Truthcoin ฉันทามติ) พึ่งพาสิ่งที่เป็นข้อสันนิษฐานด้านความปลอดภัยใหม่และไม่ผ่านการทดสอบ – ว่าใคร ๆ ก็สามารถพึ่งพาผู้คนที่ทำหน้าที่ได้อย่างซื่อสัตย์ในเกมฉันทามติพร้อมกันเพียงเพราะพวกเขาเชื่อว่าทุกคนจะ – ปัญหาที่เกิดขึ้นกับปัญหาที่เพิ่มขึ้นอย่างต่อเนื่อง ในทางกลับกันการโจมตีนี้แสดงให้เห็นถึงปัญหาพื้นฐานมากขึ้น
สถานการณ์มีการอธิบายดังนี้ สมมติว่ามีเกม schelling ง่าย ๆ ที่ผู้ใช้ลงคะแนนว่าข้อเท็จจริงบางอย่างเป็นจริงหรือไม่ (1) หรือเท็จ (0); พูดในตัวอย่างของเราว่ามันเป็นเท็จจริงๆ ผู้ใช้แต่ละคนสามารถลงคะแนน 1 หรือ 0 หากผู้ใช้โหวตเช่นเดียวกับคนส่วนใหญ่พวกเขาจะได้รับรางวัล P; มิฉะนั้นพวกเขาจะได้รับ 0 ดังนั้นเมทริกซ์ผลตอบแทนจะมีลักษณะดังนี้:
| คุณโหวต 0 | คุณโหวต 1 | |
| คนอื่นโหวต 0 | P | 0 |
| คนอื่นโหวต 1 | 0 | P |
ทฤษฎีคือถ้าทุกคนคาดหวังให้ทุกคนลงคะแนนเสียงตามความเป็นจริงแล้วสิ่งจูงใจของพวกเขาก็คือการลงคะแนนเสียงตามความเป็นจริงเพื่อให้สอดคล้องกับคนส่วนใหญ่และนั่นคือเหตุผลที่เราคาดหวังให้ผู้อื่นลงคะแนนเสียงตามความเป็นจริงในตอนแรก การเสริมแรงด้วยตนเองของ Nash Equilibrium
ตอนนี้การโจมตี สมมติว่าผู้โจมตีกระทำอย่างน่าเชื่อถือ (เช่นผ่านสัญญา Ethereum โดยเพียงแค่ให้ชื่อเสียงในการเดิมพันหรือใช้ประโยชน์จากชื่อเสียงของผู้ให้บริการ escrow ที่เชื่อถือได้) เพื่อจ่าย x ให้กับผู้ลงคะแนนที่โหวต 1 หลังจากเกมจบลงที่ x = p + ε
| คุณโหวต 0 | คุณโหวต 1 | |
| คนอื่นโหวต 0 | P | P + ε |
| คนอื่นโหวต 1 | 0 | P |
ดังนั้นจึงเป็นกลยุทธ์ที่โดดเด่นสำหรับทุกคนที่จะลงคะแนน 1 ไม่ว่าคุณจะคิดว่าคนส่วนใหญ่จะทำอะไร ดังนั้นสมมติว่าระบบไม่ได้ถูกครอบงำโดยผู้เห็นแก่ประโยชน์คนส่วนใหญ่จะลงคะแนน 1 และดังนั้นผู้โจมตีจะไม่จำเป็นต้องจ่ายอะไรเลย การโจมตีได้ประสบความสำเร็จในการจัดการกลไกโดยไม่มีค่าใช้จ่าย โปรดทราบว่าสิ่งนี้แตกต่างจากข้อโต้แย้งของ Nicholas Houy เกี่ยวกับ การโจมตีแบบไม่มีค่าใช้จ่าย 51% ในการพิสูจน์สเตค (อาร์กิวเมนต์ที่ขยายได้ทางเทคนิคไปยังหลักฐานการทำงานที่ใช้ ASIC) ในที่นี้ไม่มี การครอบครอง Epistemic จำเป็นต้องมี; แม้ว่าทุกคนจะยังคงตายในความเชื่อมั่นว่าผู้โจมตีกำลังจะล้มเหลวแรงจูงใจของพวกเขายังคงลงคะแนนเพื่อสนับสนุนผู้โจมตีเพราะผู้โจมตีเสี่ยงต่อความล้มเหลวของตัวเอง
แผนการช่วยกู้
มีช่องทางไม่กี่แห่งที่เราสามารถพยายามกอบกู้กลไก schelling วิธีการหนึ่งคือแทนที่จะเป็นรอบ N ของฉันทามติเชลลิงเองตัดสินใจว่าใครได้รับรางวัลตามหลักการ “เสียงข้างมากที่ถูกต้อง” เราใช้รอบ N + 1 เพื่อพิจารณาว่าใครควรได้รับรางวัลในช่วงรอบ N โดยมีดุลยภาพเริ่มต้นที่มีเพียงคนที่โหวตอย่างถูกต้องในระหว่างรอบ N (ทั้งในข้อเท็จจริงที่เกิดขึ้นจริง ในทางทฤษฎีสิ่งนี้ต้องการผู้โจมตีที่ต้องการทำการโจมตีแบบไม่เสียค่าใช้จ่ายเพื่อการเสียหายไม่ใช่แค่รอบเดียว แต่ยังรวมถึงรอบในอนาคตทั้งหมดทำให้เงินฝากเงินทุนที่ผู้โจมตีต้องทำ
อย่างไรก็ตามวิธีการนี้มีข้อบกพร่องสองประการ ประการแรกกลไกนั้นเปราะบาง: หากผู้โจมตีจัดการกับการทำลายรอบในอนาคตอันไกลโพ้นโดยการจ่ายเงินให้กับทุกคนโดยไม่คำนึงว่าใครจะชนะแล้วความคาดหวังของรอบที่เสียหายนั้นทำให้เกิดแรงจูงใจให้ร่วมมือกับผู้โจมตี ดังนั้นการเสียหายรอบหนึ่งนั้นมีค่าใช้จ่ายสูง แต่การทำลายรอบหลายพันรอบนั้นไม่ได้มีค่าใช้จ่ายมากนัก
ประการที่สองเนื่องจาก การลดราคาเงินฝากที่จำเป็นเพื่อเอาชนะโครงการไม่จำเป็นต้องไม่มีที่สิ้นสุด มันต้องมีขนาดใหญ่มาก (เช่น. สัดส่วนผกผันกับอัตราดอกเบี้ยที่แพร่หลาย) แต่ถ้าสิ่งที่เราต้องการคือการให้สินบนขั้นต่ำที่จำเป็นต้องมีขนาดใหญ่ขึ้นก็มีกลยุทธ์ที่ง่ายและดีกว่ามากสำหรับการทำเช่นนั้น เป็นผู้บุกเบิกโดย Paul Storcz: กำหนดให้ผู้เข้าร่วมวางเงินมัดจำขนาดใหญ่และสร้างกลไกที่ยิ่งมีการโต้แย้งมากเท่าไหร่ก็ยิ่งมีเงินทุนมากขึ้นเท่านั้น ที่ขีด จำกัด ซึ่งมีคะแนนโหวตมากกว่า 50% เล็กน้อยเป็นที่โปรดปรานของผลลัพธ์หนึ่งและ 50% ในความโปรดปรานของคนอื่น ๆ เงินฝากทั้งหมดที่นำออกไปจากผู้มีสิทธิเลือกตั้งของชนกลุ่มน้อย สิ่งนี้ทำให้มั่นใจได้ว่าการโจมตียังคงใช้งานได้ แต่ตอนนี้สินบนจะต้องมากกว่าเงินฝาก (ประมาณเท่ากับการจ่ายเงินหารด้วยอัตราการลดราคาทำให้เรามีประสิทธิภาพเท่ากันกับเกมรอบที่ไม่มีที่สิ้นสุด) แทนที่จะเป็นการจ่ายเงินสำหรับแต่ละรอบ ดังนั้นเพื่อที่จะเอาชนะกลไกดังกล่าวเราจะต้องสามารถพิสูจน์ได้ว่ามีความสามารถในการดึงการโจมตี 51% ออกไปและบางทีเราอาจรู้สึกสบายใจกับการสันนิษฐานว่าผู้โจมตีขนาดนั้นไม่มีอยู่จริง
อีกวิธีหนึ่งคือการพึ่งพาการประสานงาน โดยพื้นฐานแล้วการประสานงานอย่างใดอาจผ่านข้อผูกพันที่น่าเชื่อถือในการลงคะแนน A (ถ้า A คือความจริง) ที่มีความน่าจะเป็น 0.6 และ B ด้วยความน่าจะเป็น 0.4 ทฤษฎีที่ว่าสิ่งนี้จะช่วยให้ผู้ใช้ (น่าจะเป็น) อ้างว่ารางวัลกลไกและส่วนหนึ่งของการติดสินบนของผู้โจมตีในเวลาเดียวกัน สิ่งนี้ (ดูเหมือนว่าจะ) ทำงานได้ดีโดยเฉพาะในเกมที่แทนที่จะจ่ายรางวัลอย่างต่อเนื่องให้กับผู้มีสิทธิเลือกตั้งส่วนใหญ่ที่สอดคล้องกันแต่ละคนเกมมีโครงสร้างที่จะมีผลตอบแทนรวมอย่างต่อเนื่องปรับการจ่ายเงินรายบุคคลเพื่อให้บรรลุเป้าหมายนี้ ในสถานการณ์เช่นนี้จากมุมมองของความมีเหตุผลโดยรวมเป็นกรณีที่กลุ่มได้รับผลกำไรสูงสุดโดยมีสมาชิก 49% โหวต B เพื่อเรียกร้องรางวัลของผู้โจมตีและ 51% โหวต A เพื่อให้แน่ใจว่ารางวัลของผู้โจมตีจะจ่ายออกไป
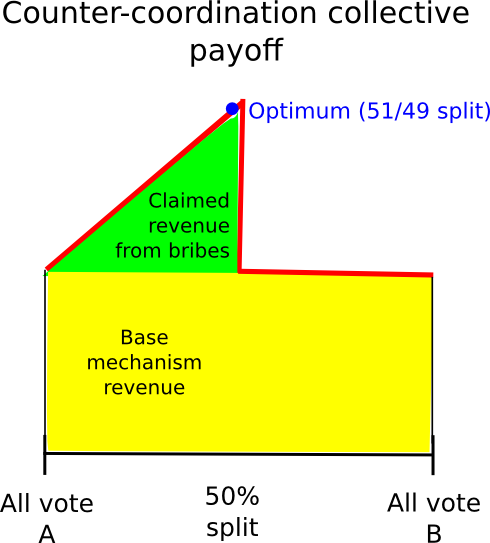
อย่างไรก็ตามวิธีการนี้เองได้รับความทุกข์ทรมานจากข้อบกพร่องที่หากสินบนของผู้โจมตีสูงพอแม้จะมีข้อบกพร่อง ปัญหาพื้นฐานคือการได้รับกลยุทธ์ผสมที่น่าจะเป็นระหว่าง A และ B สำหรับการส่งคืนแต่ละครั้งจะเปลี่ยนแปลง (เกือบ) เชิงเส้นตรงกับพารามิเตอร์ความน่าจะเป็น ดังนั้นหากสำหรับแต่ละบุคคลมันสมเหตุสมผลที่จะลงคะแนนสำหรับ B มากกว่าสำหรับ A มันจะทำให้รู้สึกถึงการลงคะแนนด้วยความน่าจะเป็น 0.51 สำหรับ B มากกว่าความน่าจะเป็น 0.49 สำหรับ B และการลงคะแนนด้วยความน่าจะเป็น 1 สำหรับ B จะทำงานได้ดียิ่งขึ้น
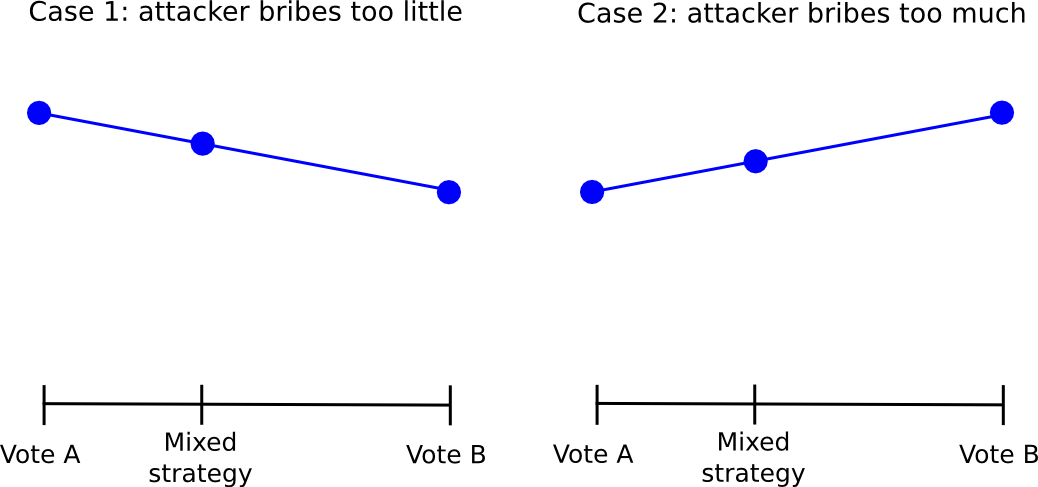
ดังนั้นทุกคนจะบกพร่องจากกลยุทธ์ “49% สำหรับ 1” โดยเพียงแค่ลงคะแนนเป็น 1 เสมอและ 1 จะชนะและผู้โจมตีจะประสบความสำเร็จในการครอบครองที่ไร้ค่าใช้จ่าย ความจริงที่ว่าแผนการที่ซับซ้อนเช่นนี้มีอยู่และเข้ามาใกล้กับ “ดูเหมือนจะทำงาน” แสดงให้เห็นว่าบางทีในอนาคตอันใกล้นี้มีรูปแบบการประสานงานที่ซับซ้อนบางอย่างจะเกิดขึ้นจริง อย่างไรก็ตามเราจะต้องเตรียมพร้อมสำหรับเหตุการณ์ที่ไม่แน่นอนที่จะไม่มีการพัฒนารูปแบบดังกล่าว
ผลที่ตามมาเพิ่มเติม
ด้วยจำนวนกลไก cryptoeconomic ที่ Schellingcoin เป็นไปได้และความสำคัญของแผนการดังกล่าวในความพยายาม “ปราศจากความน่าเชื่อถือ” อย่างหมดจดในการสร้างความเชื่อมโยงระหว่างโลก cryptographic และโลกแห่งความเป็นจริง อย่างไรก็ตามสิ่งที่น่าสนใจยิ่งกว่าคือกลไกที่ใหญ่กว่ามากที่ดูเหมือนจะไม่เหมือน schellingcoin ในตอนแรก แต่ในความเป็นจริงมีชุดของจุดแข็งและจุดอ่อนที่คล้ายกันมาก
โดยเฉพาะอย่างยิ่งให้เราชี้ไปที่ตัวอย่างที่เฉพาะเจาะจงอย่างหนึ่ง: หลักฐานการทำงาน หลักฐานการทำงานในความเป็นจริงเกมหลายสมดุลในลักษณะเดียวกับที่แผนการของ Schelling คือ: ถ้ามีสองส้อม A และ B จากนั้นถ้าคุณขุดบนส้อมที่จบลงด้วยการชนะคุณจะได้รับ 25 btc และถ้าคุณขุดบนส้อม
| คุณของฉันใน | คุณของฉันใน B | |
| คนอื่น ๆ ของฉันใน | 25 | 0 |
| คนอื่น ๆ ของฉันใน B | 0 | 25 |
ตอนนี้สมมติว่าผู้โจมตีเปิดการโจมตีสองครั้งกับหลาย ๆ ฝ่ายพร้อมกัน (ข้อกำหนดนี้ทำให้มั่นใจได้ว่าไม่มีฝ่ายเดียวที่มีแรงจูงใจที่แข็งแกร่งมากที่จะต่อต้านผู้โจมตีฝ่ายค้านแทนที่จะกลายเป็นสาธารณชนที่ดี อย่างไรก็ตามผู้โจมตีมุ่งมั่นที่จะจ่ายเงิน 25.01 BTC ให้กับทุกคนที่ทำเหมืองใน B หาก B จบลงด้วยการสูญเสีย ดังนั้นเมทริกซ์ผลตอบแทนจึงกลายเป็น:
| คุณของฉันใน | คุณของฉันใน B | |
| คนอื่น ๆ ของฉันใน | 25 | 25.01 |
| คนอื่น ๆ ของฉันใน B | 0 | 25 |
ดังนั้นการขุดบน B จึงเป็นกลยุทธ์ที่โดดเด่นโดยไม่คำนึงถึงความเชื่อของ epistemic และทุกคนทำเหมืองใน B และดังนั้นผู้โจมตีจึงชนะและจ่ายอะไรเลย โดยเฉพาะอย่างยิ่งโปรดทราบว่าในการพิสูจน์การทำงานเราไม่มีเงินฝากดังนั้นระดับของสินบนที่ต้องการเป็นสัดส่วนเฉพาะกับรางวัลการขุดคูณด้วยความยาวส้อมไม่ใช่ต้นทุนเงินทุน 51% ของอุปกรณ์การขุดทั้งหมด ดังนั้นจากจุดยืนความปลอดภัยทางเศรษฐศาสตร์ cryptoeconomic เราสามารถบอกได้ว่าการพิสูจน์การทำงานนั้นแทบจะไม่มีอัตรากำไรขั้นต้น บทความนี้โดย Andrew Poelstraอย่าลังเลที่จะเชื่อมโยงพวกเขาที่นี่เพื่อตอบสนอง) หากมีใครรู้สึกอึดอัดอย่างแท้จริงกับไฟล์ ความเป็นส่วนตัวที่อ่อนแอ เงื่อนไขของการพิสูจน์สเตคบริสุทธิ์จากนั้นตามมาว่าการแก้ปัญหาที่ถูกต้องอาจเป็นการเพิ่มหลักฐานการทำงานด้วยการพิสูจน์ไฮบริดของสเตคโดยการเพิ่มเงินฝากความปลอดภัยและการลงคะแนนเสียงสองครั้งในการขุด
แน่นอนในทางปฏิบัติหลักฐานการทำงานรอดชีวิตมาได้แม้จะมีข้อบกพร่องนี้และแน่นอนว่ามันอาจจะยังคงอยู่รอดต่อไปเป็นเวลานาน อาจเป็นกรณีที่มีระดับสูงพอที่จะเห็นแก่ผู้อื่นที่ผู้โจมตีไม่เชื่อจริง 100% ว่าพวกเขาจะประสบความสำเร็จ – แต่ถ้าเราได้รับอนุญาตให้พึ่งพาการเห็นแก่ประโยชน์ผู้อื่น ดังนั้นแผนการ Schelling ก็อาจจะจบลงด้วยการทำงานในทางปฏิบัติแม้ว่าพวกเขาจะไม่ได้ฟังดูดีในทางทฤษฎี
ส่วนต่อไปของโพสต์นี้จะหารือเกี่ยวกับแนวคิดของกลไก “อัตนัย” ในรายละเอียดเพิ่มเติมและวิธีที่พวกเขาสามารถใช้ในการแก้ไขปัญหาเหล่านี้ในทางทฤษฎี