ความสำเร็จในการลงทุนในตำนานของ Warren Buffett เกิดจากการประยุกต์ใช้หลักการทางคณิตศาสตร์ของเขาในการลงทุนในตลาดหุ้น ในขณะที่เขามีชื่อเสียงกล่าวว่าคณิตศาสตร์ที่ซับซ้อนไม่จำเป็นสำหรับการลงทุนที่ประสบความสำเร็จกลยุทธ์การสร้างความมั่งคั่งของเขาอย่างต่อเนื่องอาศัยแนวคิดทางคณิตศาสตร์ขั้นพื้นฐานที่เรียบง่ายซึ่งให้กรอบระบบอย่างเป็นระบบสำหรับการประเมินโอกาสและการจัดการความเสี่ยง นี่คือกฎคณิตศาสตร์สิบประการที่ทำให้วอร์เรนบัฟเฟตต์เป็นมหาเศรษฐี
1. สูตรดอกเบี้ยทบต้น
บัฟเฟตต์ค้นพบพลังแห่งความสนใจในช่วงต้นชีวิตเข้าใจว่าเวลาเปลี่ยนการลงทุนเล็กน้อยให้เป็นความมั่งคั่งที่ไม่ธรรมดาผ่านสูตรทางคณิตศาสตร์ A = P (1 + R/N)^nt สมการนี้แสดงให้เห็นว่าจำนวนเงินหลักอัตราดอกเบี้ยความถี่การผสมและเวลาเพิ่มขึ้นแบบทวีคูณ บัฟเฟตต์เรียกว่าดอกเบี้ยทบต้นที่แปดของความมหัศจรรย์ของโลกโดยเน้นว่าการเริ่มต้นก่อนกำหนดส่วนประกอบเวลาในสมการ
ความงามทางคณิตศาสตร์ของการผสมผสานนั้นอยู่ในการได้รับผลตอบแทนไม่เพียง แต่จากการลงทุนดั้งเดิมของคุณเท่านั้น แต่ยังได้รับผลกำไรที่สะสมไว้ก่อนหน้านี้ทั้งหมด การลงทุน $ 10,000 ที่ได้รับ 10% ต่อปีจะกลายเป็น $ 11,000 หลังจากหนึ่งปี แต่ผลตอบแทน 10% ของปีที่สองใช้กับ $ 11,000 เต็มสร้าง $ 12,100
ในช่วงหลายทศวรรษที่ผ่านมาเอฟเฟกต์การเร่งความเร็วนี้ได้กลายเป็นเรื่องน่าทึ่งซึ่งอธิบายถึงความชอบของบัฟเฟตต์สำหรับการซื้อและถือ บริษัท ที่มีคุณภาพเป็นระยะเวลานานมากกว่าการซื้อขายบ่อยครั้ง กฎนี้ใช้กับการรวมกำไรจากการลงทุนและเงินปันผลที่นำกลับมาลงทุนใหม่ซึ่งบัฟเฟตต์ได้รับการปรับให้เหมาะสม
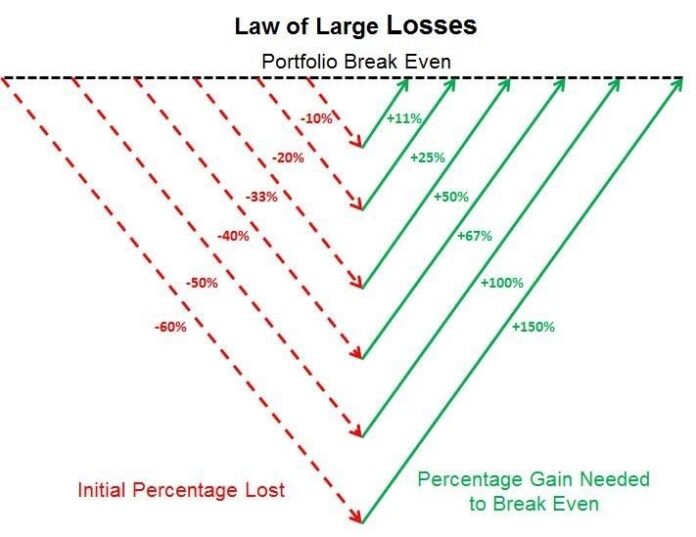
2. การสูญเสีย 50% เท่ากับกฎการกู้คืนที่ได้รับ 100%
หลักการที่มีชื่อเสียงของบัฟเฟตต์ “ อย่าเสียเงิน” ลำต้นจากความไม่สมดุลทางคณิตศาสตร์ของการสูญเสียและกำไร เมื่อการลงทุนสูญเสีย 50% ของมูลค่ามันต้องการกำไร 100% ที่จะหยุดพัก ความเป็นจริงทางคณิตศาสตร์นี้รุนแรงมากขึ้นด้วยการสูญเสียที่มากขึ้น: การลดลง 75% ต้องการกำไร 300% สำหรับการกู้คืนในขณะที่การสูญเสีย 90% ต้องการกำไร 900%
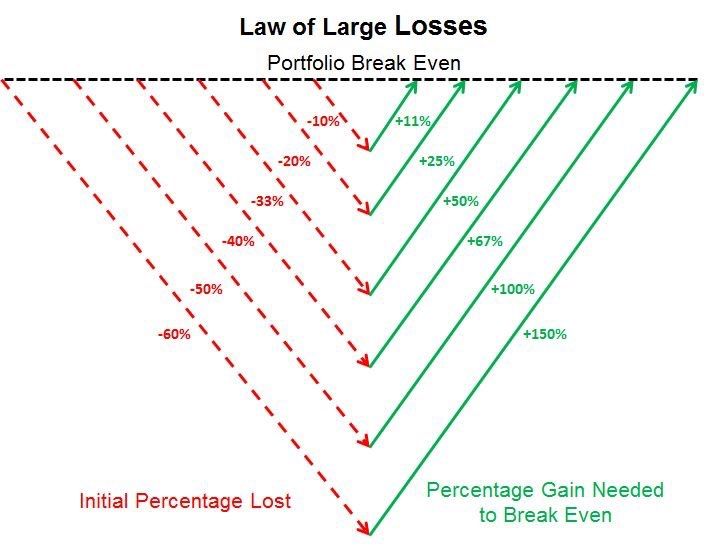
ข้อเสียทางคณิตศาสตร์นี้อธิบายวิธีการอนุรักษ์ของบัฟเฟตต์ในการบริหารความเสี่ยง แทนที่จะไล่ล่าโอกาสที่มีความเสี่ยงสูงและให้รางวัลสูงเขามุ่งเน้นไปที่การรักษาเงินทุนโดยการลงทุนใน บริษัท ที่มีรายได้ที่คาดการณ์ได้และความได้เปรียบในการแข่งขันที่สำคัญ
คณิตศาสตร์แสดงให้เห็นอย่างชัดเจนว่าการหลีกเลี่ยงการสูญเสียที่สำคัญมีส่วนช่วยในการสร้างความมั่งคั่งในระยะยาวมากกว่าการตีวิ่งกลับบ้านเป็นครั้งคราวในขณะที่ทุกข์ทรมานอย่างมาก
3. กฎกระแสเงินสดส่วนลด
บัฟเฟตต์กำหนดมูลค่าที่แท้จริงโดยการคำนวณมูลค่าปัจจุบันของกระแสเงินสดในอนาคตของ บริษัท โดยใช้การวิเคราะห์กระแสเงินสดลดราคา สูตร IV = σ (cft / (1 + r)^t) แสดงถึงผลรวมของกระแสเงินสดในอนาคตทั้งหมดหารด้วยหนึ่งบวกกับอัตราคิดลดที่เพิ่มขึ้นสู่อำนาจของช่วงเวลา วิธีการทางคณิตศาสตร์นี้ให้ความสำคัญกับ บริษัท ตามความสามารถในการสร้างเงินสดสำหรับผู้ถือหุ้นมากกว่าความเชื่อมั่นในตลาดหรือการเก็งกำไร
บัฟเฟตต์กำหนด“ รายได้ของเจ้าของ” เป็นรายได้สุทธิรวมทั้งค่าเสื่อมราคาและค่าตัดจำหน่ายลบค่าใช้จ่ายเงินทุนและเพิ่มเติม การทำงาน ความต้องการเงินทุน การคำนวณนี้ให้ภาพเงินสดที่แม่นยำยิ่งขึ้นสำหรับผู้ถือหุ้น ด้วยการเปรียบเทียบมูลค่าที่แท้จริงนี้กับราคาตลาดปัจจุบันบัฟเฟตต์ระบุโอกาสที่ต่ำกว่าที่การวิเคราะห์ทางคณิตศาสตร์แสดงให้เห็นว่าหุ้นซื้อขายต่ำกว่ามูลค่าพื้นฐาน
4. กฎการเพิ่มประสิทธิภาพค่าใช้จ่ายโอกาส
การตัดสินใจลงทุนทุกครั้งเกี่ยวข้องกับค่าใช้จ่ายโอกาส – ผลตอบแทนก่อนหน้านี้โดยเลือกการลงทุนหนึ่งรายการมากกว่าทางเลือกอื่น บัฟเฟตต์ใช้การคิดทางคณิตศาสตร์โดยการเปรียบเทียบผลตอบแทนที่อาจเกิดขึ้นกับโอกาสที่แตกต่างกันอย่างต่อเนื่องแม้ในอุตสาหกรรมที่ไม่เกี่ยวข้อง กระบวนการปรับให้เหมาะสมนี้ต้องการการประเมินผลตอบแทนที่ปรับความเสี่ยงเพื่อจัดสรรเงินทุนให้กับโอกาสที่น่าดึงดูดที่สุด
วิธีการของบัฟเฟตต์เกี่ยวข้องกับการสร้างอัตราอุปสรรค์ทางจิตที่การลงทุนต้องเกินกว่าที่จะพิจารณา เมื่อประเมินการซื้อหุ้นที่มีศักยภาพเขาจะเปรียบเทียบผลตอบแทนที่คาดหวังจากพันธบัตรหุ้นอื่น ๆ และ เก็บเงินสด– กรอบการทำงานทางคณิตศาสตร์นี้ช่วยให้มั่นใจว่าเงินทุนไหลไปสู่โอกาสที่นำเสนอผลตอบแทนที่ปรับความเสี่ยงได้ดีที่สุดแทนที่จะเป็นตัวเลือกที่คุ้นเคยหรือสะดวกที่สุด
5. กฎความเข้มข้น 5/25
บัฟเฟตต์สนับสนุนการลงทุนในความคิดที่ดีที่สุดของคุณมากกว่าการกระจายความหลากหลายในโอกาสปานกลาง วิธีการของเขาเกี่ยวข้องกับการจดทะเบียนการลงทุนที่มีศักยภาพระบุตัวเลือกที่น่าสนใจที่สุดห้าอันดับแรกและมุ่งเน้นไปที่ผู้ที่หลีกเลี่ยงการล่อลวงเพื่อติดตามส่วนที่เหลืออีกยี่สิบ วิธีการทางคณิตศาสตร์นี้ในการก่อสร้างพอร์ตโฟลิโอตระหนักดีว่าการกระจายความเสี่ยงสามารถเจือจางผลตอบแทนเมื่อนำไปใช้มากเกินไป
คณิตศาสตร์ของสมาธิทำงานเนื่องจาก บริษัท พิเศษสร้างผลตอบแทนที่เกินกว่าที่นักแสดงเฉลี่ยไม่สามารถจับคู่ได้ ในขณะเดียวกันการกระจายความเสี่ยงลดความผันผวน แต่ จำกัด ศักยภาพกลับหัวกลับหางเมื่อคุณเชื่อในโอกาสที่เหนือกว่าอย่างแท้จริง วิธีการที่เข้มข้นของบัฟเฟตต์ต้องมีการวิเคราะห์อย่างละเอียด แต่ช่วยให้การผสมผสานทางคณิตศาสตร์สามารถทำงานกับความคิดที่ดีที่สุดของคุณได้มากกว่าที่จะลดการลงทุนโดยเฉลี่ยจำนวนมาก
6. กฎผลตอบแทนของผู้ถือหุ้น
ผลตอบแทนจากการวัดส่วนของ บริษัท ที่ บริษัท สร้างผลกำไรจากผู้ถือหุ้นได้อย่างมีประสิทธิภาพ: ROE = รายได้สุทธิ÷ส่วนของผู้ถือหุ้น บัฟเฟตต์แสวงหา บริษัท ที่มี ROE สูงอย่างสม่ำเสมอซึ่งบ่งบอกถึงความสามารถของผู้บริหารในการสร้างมูลค่าจากการลงทุน ตัวชี้วัดทางคณิตศาสตร์นี้แสดงให้เห็นว่า บริษัท ต่างๆปรับใช้เงินผู้ถือหุ้นเพื่อสร้างรายได้อย่างไร
บริษัท ที่มี ROE สูงอย่างยั่งยืนมีข้อได้เปรียบในการแข่งขันที่อนุญาตให้พวกเขาได้รับผลตอบแทนที่เหนือกว่าจากการลงทุน ธุรกิจเหล่านี้มักจะต้องมีการลงทุนเพิ่มเติมน้อยที่สุดเพื่อให้พวกเขาสามารถมีความมั่งคั่งของผู้ถือหุ้นผสมได้อย่างมีประสิทธิภาพ
การมุ่งเน้นของบัฟเฟตต์เกี่ยวกับ ROE สะท้อนให้เห็นถึงความเข้าใจทางคณิตศาสตร์ของเขาว่าธุรกิจที่สร้างผลตอบแทนสูงต่อผู้ถือหุ้นสร้างมูลค่ามากกว่าที่ต้องการเงินทุนคงที่เพื่อรักษาการเติบโต
7. ขอบของกฎความปลอดภัย
บัฟเฟตต์ซื้อหุ้นเมื่อพวกเขาซื้อขายต่ำกว่ามูลค่าที่คำนวณได้อย่างมีนัยสำคัญสร้างอัตรากำไรขั้นต้นของความปลอดภัยที่แสดงเป็นมูลค่าที่แท้จริงลบด้วยราคาตลาด บัฟเฟอร์ทางคณิตศาสตร์นี้ป้องกันข้อผิดพลาดในการวิเคราะห์สถานการณ์ที่ไม่คาดฝันและความผันผวนของตลาด ยิ่งอัตรากำไรขั้นต้นมีขนาดใหญ่เท่าใดการป้องกันการสูญเสียเงินทุนถาวรก็ยิ่งมากขึ้นเท่านั้น
หลักการนี้สืบทอดมาจาก เบนจามินเกรแฮมตระหนักว่าการวิเคราะห์การลงทุนเกี่ยวข้องกับการประมาณการและสมมติฐานที่อาจพิสูจน์ได้ว่าไม่ถูกต้อง บัฟเฟตต์ลดความน่าจะเป็นของการสูญเสียอย่างมีนัยสำคัญในขณะที่เพิ่มผลตอบแทนที่อาจเกิดขึ้นโดยต้องการเบาะทางคณิตศาสตร์ที่สำคัญระหว่างมูลค่าที่แท้จริงและราคาซื้อ ระยะขอบของความปลอดภัยเปลี่ยนการลงทุนจากการเก็งกำไรเป็นแบบฝึกหัดทางคณิตศาสตร์ที่มีอัตราต่อรองที่ดี
8. กฎการเปรียบเทียบตัวเลข
บัฟเฟตพัฒนา การรู้หนังสือเชิงตัวเลขโดยการวิเคราะห์งบการเงินอย่างต่อเนื่องและสร้างฐานข้อมูลทางจิตของตัวชี้วัดทางธุรกิจ วิธีการเชิงปริมาณนี้ช่วยให้การเปรียบเทียบโอกาสการลงทุนอย่างรวดเร็วโดยการประเมินอัตราส่วนสำคัญอัตราการเติบโตและลักษณะทางการเงินอย่างรวดเร็ว กรอบทางคณิตศาสตร์กลายเป็นลักษณะที่สองผ่านการวิเคราะห์ซ้ำ ๆ ของ บริษัท หลายร้อยแห่ง
ความคล่องแคล่วเชิงตัวเลขนี้ช่วยให้สามารถจดจำรูปแบบได้ในอุตสาหกรรมและช่วงเวลา บัฟเฟตต์สามารถเปรียบเทียบตัวชี้วัดทางการเงินกับ บริษัท ที่คล้ายกันและแบบอย่างในอดีตได้ทันทีเมื่อประเมินการลงทุนที่มีศักยภาพ วิธีการทางคณิตศาสตร์นี้เปลี่ยนการวิเคราะห์ธุรกิจที่ซับซ้อนเป็นการเปรียบเทียบอย่างเป็นระบบของปัจจัยเชิงปริมาณที่บ่งบอกถึงความน่าดึงดูดการลงทุนระยะยาว
9. กฎความน่าจะเป็นสูง
บัฟเฟตต์มุ่งเน้นไปที่สถานการณ์การลงทุนที่มีความน่าจะเป็นสูงแทนที่จะพยายามทำนายผลลัพธ์ที่ไม่แน่นอน วิธีการทางคณิตศาสตร์นี้ตระหนักว่าข้อมูลที่สมบูรณ์แบบนั้นเป็นไปไม่ได้ แต่บางสถานการณ์ให้ความสำเร็จที่ดีกว่าความสำเร็จอย่างมาก เขาปรับปรุงความน่าจะเป็นทางคณิตศาสตร์ของผลลัพธ์ที่ดีโดยมุ่งเน้นไปที่ธุรกิจที่คาดการณ์ได้ด้วยความได้เปรียบในการแข่งขันที่ทนทาน
คณิตศาสตร์ของความน่าจะเป็นทำงานในการลงทุนเนื่องจากข้อได้เปรียบเล็กน้อยจำนวนมากรวมกันเมื่อเวลาผ่านไป แทนที่จะต้องการความมั่นใจเกี่ยวกับผลลัพธ์ที่เฉพาะเจาะจงวิธีการนี้แสวงหาสถานการณ์ที่มีหลายปัจจัยที่แนะนำอัตราต่อรองที่ดี การประยุกต์ใช้การคิดตามความน่าจะเป็นอย่างต่อเนื่องสร้างขอบคณิตศาสตร์ที่สะสมเป็นความมั่งคั่งมากมายมานานหลายทศวรรษ
10. กฎขอบคณิตศาสตร์
บัฟเฟตต์ให้การลงทุนเฉพาะเมื่อการวิเคราะห์ทางคณิตศาสตร์แสดงให้เห็นถึงผลลัพธ์ที่คาดหวัง ขอบนี้อาจเป็นความน่าจะเป็น 55% ของความสำเร็จเมื่อเทียบกับความน่าจะเป็นของการสูญเสีย 45% แต่เมื่อนำไปใช้อย่างต่อเนื่องในการตัดสินใจหลายครั้งข้อได้เปรียบทางคณิตศาสตร์ขนาดเล็กจะรวมกันเป็นผลงานที่มีประสิทธิภาพสูงกว่าอย่างมีนัยสำคัญ กุญแจสำคัญคือการมีข้อได้เปรียบในการวิเคราะห์ที่แท้จริงมากกว่าการพึ่งพาโชคหรือการเก็งกำไร
ขอบคณิตศาสตร์นี้เกิดจากการวิเคราะห์ที่เหนือกว่าระยะเวลาที่ยาวนานขึ้นและวินัยทางอารมณ์ในช่วงความผันผวนของตลาด ในขณะที่การลงทุนรายบุคคลอาจไม่ประสบความสำเร็จเสมอไป แต่กฎหมายทางคณิตศาสตร์ของจำนวนมากทำให้มั่นใจได้ว่าการใช้ขอบเล็กน้อยจะให้ผลลัพธ์ระยะยาวที่เหนือกว่า ความสำเร็จของบัฟเฟตต์แสดงให้เห็นว่าการคิดทางคณิตศาสตร์ใช้กับการลงทุนสร้างความได้เปรียบในการแข่งขันอย่างยั่งยืน
บทสรุป
ความมั่งคั่งที่ไม่ธรรมดาของ Warren Buffett เป็นผลมาจากการใช้หลักการทางคณิตศาสตร์อย่างต่อเนื่องในการตัดสินใจลงทุน กฎเหล่านี้แสดงให้เห็นว่าการลงทุนที่ประสบความสำเร็จนั้นต้องการการวิเคราะห์เชิงปริมาณการคิดความน่าจะเป็นและวินัยทางคณิตศาสตร์มากกว่าสูตรที่ซับซ้อนหรือเวลาในตลาดตามการคาดการณ์และความคิดเห็น
ด้วยการทำความเข้าใจและใช้แนวคิดทางคณิตศาสตร์เหล่านี้นักลงทุนสามารถสร้างความมั่งคั่งด้วยวิธีการที่เป็นระบบเดียวกันซึ่งสร้างหนึ่งในโชคชะตาที่ยิ่งใหญ่ที่สุดของประวัติศาสตร์