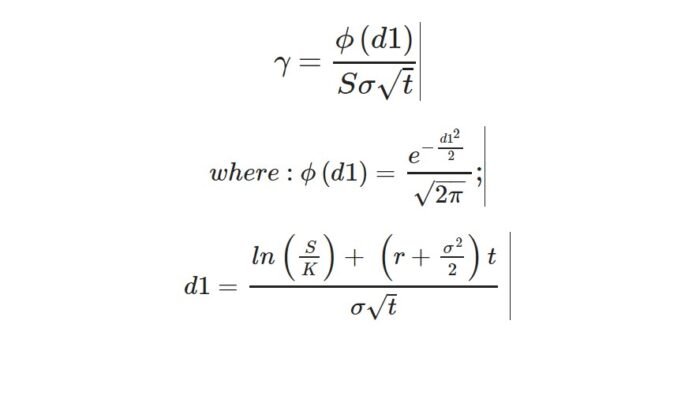ตัวเลือกแกมมาอธิบาย: ความไวของเดลต้าต่อราคา

ชาวกรีกอันดับสองนั้นซับซ้อนกว่าเล็กน้อย แทนที่จะพิจารณาถึงผลกระทบที่มีต่อออปชั่น พวกเขาวัดว่าการเปลี่ยนแปลงในพารามิเตอร์พื้นฐานตัวใดตัวหนึ่งที่เหมือนกันนำไปสู่การเปลี่ยนแปลงค่าของกรีกลำดับที่หนึ่งอย่างไร

ตัวชี้วัดลำดับที่สองที่สำคัญคือแกมมา ในความเป็นจริง มันเป็นภาษากรีกอันดับสองเพียงแห่งเดียวที่เทรดเดอร์ออปชั่นใช้อย่างสม่ำเสมอ Gamma จะวัดอัตราการเปลี่ยนแปลงของเดลต้าที่เกี่ยวข้องกับสินทรัพย์อ้างอิง

เนื่องจากเดลต้าเป็นอนุพันธ์อันดับหนึ่งของราคาของออปชัน แกมม่าจึงเป็นอนุพันธ์อันดับสอง

เพื่อทำความเข้าใจว่าทั้งหมดนี้หมายถึงอะไร ก่อนอื่นเราต้องย้อนกลับไปและกำหนดว่าเดลต้าของตัวเลือกคืออะไร

ทำความเข้าใจกับเดลต้า

ตัวเลือกคณิตศาสตร์แกมมา

ไม่จำเป็นต้องเข้าใจคณิตศาสตร์เบื้องหลังแกมมา (โปรดไปที่หัวข้อถัดไปหากต้องการ) แต่สำหรับผู้สนใจแกมมาได้รับการนิยามอย่างเป็นทางการว่าเป็นอนุพันธ์บางส่วนของเดลต้าเมื่อเทียบกับราคาหุ้นอ้างอิง

สูตรอยู่ด้านล่าง (ต้องมีความรู้บางอย่างเกี่ยวกับการแจกแจงแบบปกติจึงจะเข้าใจได้)

เดลต้าหมายถึงการเปลี่ยนแปลงราคาของตัวเลือกที่เกี่ยวข้องกับราคาของหลักทรัพย์อ้างอิง สำหรับการโทร เดลต้าจะมีค่าตั้งแต่ 0 ถึง 1

สำหรับการวาง จะมีค่าเป็น -1 และ 0 เดลต้าแสดงว่าราคาของออปชั่นเพิ่มขึ้นหรือลดลงเท่าใดเมื่อสินทรัพย์อ้างอิงเคลื่อนไหว 1 จุด

โดยปกติ เมื่อออปชั่นอยู่ที่เงิน คุณสามารถคาดหวังที่จะเห็นค่าเดลต้าระหว่าง 0.5 ถึง -0.5 เมื่อออปชันไม่มีเงินมากนัก ก็จะมีค่าเดลต้าใกล้กับ 0 และเมื่อมีเงินลึก ค่าเดลต้าก็จะใกล้กับ 1

ซึ่งหมายความว่า โดยทั่วไปแล้ว เจ้าของสายจะทำกำไรเมื่อหุ้นอ้างอิงมีราคาเพิ่มขึ้น เนื่องจากสิ่งนี้นำไปสู่เดลต้าที่เป็นบวก ในทางตรงกันข้าม เนื่องจาก Put มีค่าเดลต้าเป็นลบ เจ้าของจึงมองเห็นกำไรเมื่อหุ้นอ้างอิงลดลง

สิ่งสำคัญคือต้องทราบว่าไม่ได้เป็นเช่นนั้นเสมอไป เมื่อปัจจัยอื่นมีขนาดใหญ่เพียงพอ ก็สามารถชดเชยข้อมูลได้

การคำนวณผลกระทบของเดลต้า

หากต้องการใช้ตัวอย่างข้างต้น ลองจินตนาการว่าการโทรมีค่าเดลต้าเท่ากับ 0.5 หากหุ้นอ้างอิงเพิ่มขึ้น 1 ดอลลาร์ ราคาของการโทรควรเพิ่มขึ้นประมาณ 0.50 ดอลลาร์

หากสินทรัพย์อ้างอิงลดลง 1 ดอลลาร์ ราคาจะลดลงประมาณ 0.50 ดอลลาร์ แน่นอนว่าสิ่งนี้ถือว่าไม่มีการเปลี่ยนแปลงตัวแปรการกำหนดราคาอื่น ๆ

ตอนนี้ลองจินตนาการว่าการวางมีเดลต้าเป็น -0.5 หากหุ้นอ้างอิงเพิ่มขึ้น 1 ดอลลาร์ ราคาที่เสนอขายจะลดลง 0.50 ดอลลาร์ หากลดลง 1 ดอลลาร์ ราคาก็จะเพิ่มขึ้น 0.50 ดอลลาร์

ผู้ถือออปชั่นจะสังเกตเห็นว่าเดลต้าของออปชั่นเพิ่มขึ้นอย่างรวดเร็วในช่วงราคาหนึ่ง ซึ่งเรียกว่าเดลต้าแบบกระจาย

สำหรับผู้ซื้อ นี่เป็นข่าวดี เนื่องจากสามารถนำไปสู่ผลกำไรมหาศาลได้ แน่นอนว่าสิ่งที่ตรงกันข้ามเกิดขึ้นกับผู้ขายที่อยู่อีกด้านหนึ่งของพื้นที่สามเหลี่ยมปากแม่น้ำที่กำลังขยายตัว

ในความเป็นจริง เดลต้าที่ระเบิดเป็นสาเหตุสำคัญว่าทำไมการขายออปชันที่ไม่มีการป้องกันความเสี่ยงจึงมีความเสี่ยงสูง

อย่างไรก็ตาม โปรดทราบว่าในขณะที่การป้องกันความเสี่ยงแบบเดลต้าสามารถลดความเสี่ยงจากการเคลื่อนไหวของราคาของสินทรัพย์อ้างอิงได้ กลยุทธ์ดังกล่าวจะลดค่าอัลฟ่าพร้อมกับแกมม่า ตอนนี้เรามาดูกันว่าทำไมมันถึงสำคัญ

แกมมาคืออะไร?

แกมมาระบุว่าเดลต้าจะเปลี่ยนแปลงไปเท่าใดเมื่อการลงทุนอ้างอิงขยับไป 1 ดอลลาร์ (หน่วยของแกมมาคือ 1/$)

กล่าวอีกนัยหนึ่ง ในขณะที่เดลต้าจะบอกคุณว่าราคาของออปชั่นจะเปลี่ยนแปลงที่ความเร็วเท่าใด แกมม่าจะบอกคุณว่าการเปลี่ยนแปลงจะเกิดขึ้นด้วยความเร่งเท่าใด

ซึ่งหมายความว่าคุณสามารถใช้แกมมาเพื่อคาดการณ์ว่าเดลต้าจะเคลื่อนไหวอย่างไรหากสินทรัพย์อ้างอิงเปลี่ยนแปลง และดังนั้นมูลค่าของออปชันจะเปลี่ยนแปลงอย่างไร

แกมมามีความสำคัญเนื่องจากเดลต้ามีประโยชน์ในช่วงเวลาหนึ่งเท่านั้น

ด้วยแกมม่า คุณสามารถทราบได้ว่าส่วนต่างของตัวเลือกควรเปลี่ยนแปลงเท่าใดในกรณีที่สินทรัพย์อ้างอิงเพิ่มขึ้นหรือลดลง

ทำไมเราถึงต้องการแกมมา?

เพื่อเน้นย้ำว่าเหตุใดแกมมาจึงมีความสำคัญ และวิธีที่แกมมาเพิ่มความเข้าใจอีกระดับให้กับตัวเลือกที่นอกเหนือไปจากเดลต้า ให้เรามาดูตัวอย่างกัน ลองนึกภาพสองตัวเลือกมีเดลต้าเหมือนกันแต่ค่าแกมม่าต่างกัน

ในตัวอย่างนี้ไม่จำเป็นต้องใช้ตัวเลขด้วยซ้ำ แค่บอกว่าอันหนึ่งมีแกมมาต่ำและอีกอันมีแกมม่าสูง

ตัวเลือกที่มีแกมม่าสูงจะมีความเสี่ยงมากกว่า เนื่องจากหากมีการเคลื่อนไหวที่ไม่เอื้ออำนวยในสินทรัพย์อ้างอิง ผลกระทบก็จะเด่นชัดมากขึ้น

กล่าวอีกนัยหนึ่ง หากออปชันมีค่าแกมม่าสูง ก็มีแนวโน้มที่จะมีการแกว่งตัวที่ผันผวนเพิ่มขึ้น เนื่องจากเทรดเดอร์ส่วนใหญ่ชอบที่จะคาดเดาออปชั่นได้ จึงควรใช้ออปชั่นที่มีแกมม่าต่ำ

อีกวิธีหนึ่งในการอธิบายสิ่งนี้คือการบอกว่าแกมมาวัดความน่าจะเป็นของตัวเลือกนั้นมีเสถียรภาพเพียงใด

แกมมาเปลี่ยนแปลงไปตามกาลเวลาอย่างไร

เนื่องจากเดลต้าของออปชั่นเป็นแบบไดนามิก แกมมาจึงต้องเปลี่ยนแปลงอยู่ตลอดเวลา แม้แต่การเคลื่อนไหวเล็กๆ น้อยๆ ของหุ้นอ้างอิงก็อาจนำไปสู่การเปลี่ยนแปลงแกมม่าได้

โดยทั่วไปแล้ว แกมม่าจะถึงค่าสูงสุดเมื่อหุ้นอยู่ใกล้ ราคานัดหยุดงาน– ดังที่เราเห็นไปแล้ว ค่าเดลต้าสูงสุดคือ 1

เมื่อค่าเดลต้าลดลงเมื่อออปชั่นเคลื่อนเข้าหรือออกจากเงิน ค่าแกมมาจะเข้าใกล้ 0 มากขึ้น

การใช้แกมมาเพื่อวัดการเปลี่ยนแปลงในเดลต้า

การคำนวณการเปลี่ยนแปลงของเดลต้าโดยใช้แกมมานั้นค่อนข้างตรงไปตรงมา ตัวอย่างเช่น สมมติว่าหุ้น ABC ซื้อขายที่ 47 ดอลลาร์ สมมุติว่าเดลต้าคือ 0.3 และแกมมาคือ 0.2

ในกรณีที่หุ้นอ้างอิงเพิ่มราคา 1 ดอลลาร์เป็น 48 ดอลลาร์ เดลต้าจะขยับขึ้นไปที่ 0.5 หากราคาหุ้นลดลง 1 ดอลลาร์เหลือ 46 ดอลลาร์ เดลต้าจะลดลงเหลือ 0.1

ตัวเลือกแบบยาวและแบบสั้นพร้อมแกมมา

สำหรับผู้ถือออปชันระยะยาว แกมม่าหมายถึงการเร่งผลกำไรทุกครั้งที่สินทรัพย์อ้างอิงขยับ $1 ไปตามความต้องการ พวกเขาคือ แกมม่ายาว–

เนื่องจากแกมมาทำให้ส่วนต่างของตัวเลือกเพิ่มขึ้นเมื่อตัวเลือกขยับเข้าใกล้เงินมากขึ้นหรือเมื่อเงินมากขึ้น

ดังนั้นการเพิ่มขึ้นของสินทรัพย์อ้างอิงทุกๆ ดอลลาร์หมายถึงผลตอบแทนจากเงินทุนที่มีประสิทธิภาพมากขึ้น

แนวคิดเดียวกันนี้หมายความว่าเมื่อสินทรัพย์อ้างอิงเคลื่อนไหว $1 ขัดกับความต้องการของผู้ถือ การขาดทุนก็จะลดลง

ในทางกลับกัน แกมม่าก่อให้เกิดความเสี่ยงสำหรับผู้ขายออปชั่น เนื่องจากหากมีผู้ชนะในสมการ ก็จะต้องมีผู้แพ้เช่นกัน เช่นเดียวกับที่แกมมาเร่งผลกำไรให้กับผู้ถือออปชั่นระยะยาว มันก็เร่งการขาดทุนให้กับผู้ขายเช่นกัน

ในทำนองเดียวกัน เนื่องจากทำให้ผู้ถือขาดทุนช้าลง จึงทำให้ผู้ขายมีทิศทางเพิ่มขึ้นและชะลอตัวลง

ความสำคัญของการพยากรณ์ที่ถูกต้อง

ไม่ว่าคุณจะซื้อหรือขาย การคาดการณ์ที่แม่นยำถือเป็นสิ่งสำคัญ ในฐานะผู้ซื้อ แกมม่าที่สูงที่คุณคาดการณ์ไม่ถูกต้องอาจหมายความว่าตัวเลือกจะเคลื่อนเข้าสู่เงิน และเดลต้าเคลื่อนไปทาง 1 เร็วกว่าที่คุณคาดไว้

นี่จะหมายความว่าสามเหลี่ยมปากแม่น้ำจะลดลงเร็วกว่าที่คุณคาดการณ์ไว้

หากคุณเป็นผู้ขาย การคาดการณ์ที่ไม่ถูกต้องก็เป็นปัญหาเช่นกัน เนื่องจากออปชันที่คุณขายจะเปลี่ยนไปเป็นเงิน แกมมาที่สูงอาจหมายความว่าตำแหน่งของคุณขัดแย้งกับคุณในอัตราที่รวดเร็ว ในกรณีที่การคาดการณ์ของคุณแม่นยำ ค่าแกมม่าที่สูงอาจหมายความว่าตัวเลือกที่ขายจะสูญเสียเงินเร็วขึ้น และให้ผลลัพธ์ที่เป็นบวกสำหรับคุณ

ความผันผวนส่งผลต่อแกมมาอย่างไร

แกมมาของออปชันที่เป็นเงินจะสูงเมื่อมีความผันผวนต่ำ เนื่องจากความผันผวนต่ำเกิดขึ้นเมื่อค่าเวลาของออปชั่นต่ำ จากนั้นคุณจะเห็นการเพิ่มขึ้นอย่างมากเมื่อหุ้นอ้างอิงใกล้ถึงราคาใช้สิทธิ

อย่างไรก็ตาม เมื่อความผันผวนอยู่ในระดับสูง แกมม่ามักจะคงที่เมื่อเทียบกับราคาใช้สิทธิ เหตุผลก็คือ เมื่อออปชั่นมีเงินอยู่ลึกๆ หรือหมดเวลา มูลค่าของเวลาก็มีแนวโน้มที่จะมีนัยสำคัญ

เมื่อออปชั่นเข้าใกล้เงิน มูลค่าเวลาที่น่าทึ่งน้อยลง ในทางกลับกัน สิ่งนี้ทำให้แกมม่ามีทั้งต่ำและคงที่

ความเสี่ยงในการหมดอายุ

อีกแง่มุมหนึ่งที่ต้องคำนึงถึงคือความเสี่ยงในการหมดอายุ ยิ่งออปชั่นใกล้หมดอายุมากเท่าไร เส้นโค้งความน่าจะเป็นก็จะยิ่งแคบลงเท่านั้น

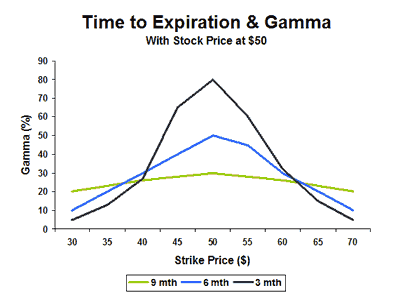
การไม่มีเวลาสำหรับสินทรัพย์อ้างอิงที่จะย้ายไปใช้การหยุดงานประท้วงที่ห่างไกลจากเงินจะช่วยลดความน่าจะเป็นที่สินทรัพย์เหล่านั้นจะอยู่ในรูปของเงิน ผลลัพธ์ที่ได้คือการกระจายเดลต้าที่แคบลงและมีแกมมาเชิงรุกมากขึ้น

วิธีที่ปลอดภัยที่สุดในการใช้ความเข้าใจเกี่ยวกับแกมมาให้เป็นประโยชน์คือการม้วนและปิดสถานะของคุณอย่างน้อยเจ็ด (หรืออาจมากถึง 10) วันก่อนหมดอายุ

หากคุณรอนานกว่าเจ็ดวัน มีโอกาสมากขึ้นที่คุณจะเห็นการเปลี่ยนแปลงที่รุนแรง โดยที่การเทรดที่สูญเสียจะแปลงเป็นผู้ชนะและในทางกลับกัน ผู้ซื้ออาจได้รับประโยชน์จากแนวโน้มนี้ แต่จะมีความเสี่ยงเป็นพิเศษสำหรับผู้ขาย

รายการกลยุทธ์เชิงบวกแกมมา

รายการกลยุทธ์เชิงลบแกมมา

• โทรสั้น

• ใส่สั้น

• คร่อมสั้น

• รัดคอสั้น

• การกระจายสินเชื่อแนวตั้ง

• เขียนการโทรที่ครอบคลุม

• เขียนแบบครอบคลุม

• แร้งเหล็ก

• ผีเสื้อ

• การแพร่กระจายปฏิทินแบบยาว

สรุป

• Gamma จะวัดอัตราการเปลี่ยนแปลงของเดลต้าตามราคาของสินทรัพย์อ้างอิง

• ออปชั่นยาวทั้งหมดมีแกมมาเป็นบวก และออปชั่นสั้นทั้งหมดมีแกมม่าเป็นลบ

• แกมมาของตำแหน่งจะบอกเราว่าการเคลื่อนไหว 1.00 ดอลลาร์ในจุดอ้างอิงจะเปลี่ยนเดลต้าของตัวเลือกอย่างไร

• เราไม่ถือการซื้อขายของเราจนกว่าจะหมดอายุเพื่อหลีกเลี่ยงความเสี่ยงแกมมาที่เพิ่มขึ้น
  

เกี่ยวกับผู้แต่ง: Chris Younger สำเร็จการศึกษาระดับปริญญาตรีสาขาคณิตศาสตร์และประสบการณ์ทางการเงิน 18 ปี คริสเป็นชาวอังกฤษโดยภูมิหลัง แต่เคยทำงานในสหรัฐอเมริกาและเมื่อเร็วๆ นี้ในออสเตรเลีย ความสนใจในออปชั่นของเขาถูกกระตุ้นครั้งแรกโดยส่วน ‘Buying and selling Choices’ ของ Monetary Occasions (ของลอนดอน) เขาตัดสินใจที่จะนำความรู้นี้ไปสู่ผู้ฟังในวงกว้างและก่อตั้ง Epsilon Choices ในปี 2012

บทความที่เกี่ยวข้อง